Петр Путенихин Правила счета элементов бесконечного множества

Связь математики и физики

Давно замечено интересное и важное свойство математики, которая позволяет делать верные, но изначально просто как бы выдуманные описания нашего мира, предсказания:

"Существует вопрос, давно волнующий людей, задумывающихся об основаниях математики: почему математика столь эффективна при описании нашего мира и столь хорошо описывает его эволюцию? … Почему эти правила так хорошо работают?" [6]

Однако вряд ли следует слишком уж сильно этому удивляться и вспоминать еще одно её такое же удивительное свойство: способность дать любой желаемый результат. Эта математика так хорошо работает просто потому, что мы и вывели её из прямых наблюдений за окружающей действительностью. Эффективно работает, значит, верно подсмотрели. Более того, в науке и, в частности, в физике уже давно замечена еще одна интересная закономерность: кажущиеся поначалу абстрактными математические выражения, уравнения вдруг оказываются описанием какого-нибудь вполне реального явления:

"… физики обнаруживают, что математические построения, необходимые им для описания нового класса явления, уже исследованы математиками по причинам, не имеющим ничего общего с обсуждаемыми явлениями" [2, с.264].

Однако даже при таком явно полезном подходе следует все-таки быть предельно осторожным при формулировке выводов и следствий из этих математических построений. Можно привести ряд примеров, когда такие выкладки приводят не просто к противоречиям со здравым смыслом, но к довольно заметным противоречиям с логикой, содержат логические ошибки. Например, одним из наиболее известных таких странных выводов при исследовании бесконечных множеств элементов являются доказательства Кантора о равенстве числа точек на квадрате и линии, равной длине его ребра.

Приведённые в статье выкладки опубликованы в авторской книге [11].

Равномощные множества чисел

В литературе по космологии встречаются весьма любопытные рассуждения о тождественных бесконечностях. В частности делается очевидный ошибочный вывод о том, что в бесконечности часть может быть равна целому:

«множество натуральных чисел (ℕ) равномощно множествам целых чисел (ℤ), чётных натуральных чисел, всех рациональных чисел (ℚ), а отрезок числовой прямой (𝕀 = [0,1], континуум) оказывается в биективном соответствии со всей числовой прямой (ℝ), а также с n-мерным евклидовым пространством (ℝⁿ)» [1].

Несомненно, это противоречит нашей интуиции. Ведь четные числа явно составляют лишь половину всех целых чисел. Это справедливо для любой конечной совокупности чисел, но, как утверждается в цитате, не соответствует бесконечным рядам, для которых получается, что их количества равны. А утверждение в отношении отрезка буквально означает, что всем точкам отрезка соответствуют все точки всей евклидовой бесконечной плоскости. Такие же странные выводы о соотношении целого и части делаются и в космологии [7, с.77; 2, с.282].

И эти противоречащие здравому смыслу и логике выводы преподносятся в научно-популярной литературе, в книгах, в документальных фильмах (BBC) как строго доказанные факты. Ошибочность подобных методов можно показать, если произвести подсчет количеств натуральных чисел при различных способах их группирования, приводящие к любому произвольному результату.

Для доказательства указанной равномощности точек отрезка и квадрата Кантор использует противоречивый, нелогичный метод. Конечно, можно предположить, что методология и доказательства Кантора и приведенные в цитате утверждения являются узкими теоретическими, частными проблемами. Однако они в явном виде использованы для того чтобы поставить под сомнение, например, одно из основных положений понятия многомерности:

"… параметрическое определение размерности (по крайней мере в форме: "Размерность пространства – это минимальное число параметров, которые необходимы, чтобы отличать точки пространства друг от друга") математически некорректно. Это стало ясно после построенного Георгом Кантором (1845—1918) знаменитого примера взаимно-однозначного соответствия между множествами точек квадрата и отрезка" [4, с.32].

Рассмотрим некоторые доказательства, которые позволят решительно отвергнуть аргументы Кантора.

Количества натуральных чисел в группах

Нумерация четных чисел. Например, в одном из вариантов для доказательства равномощности предлагается записать четные числа в виде бесконечного ряда, а под этим рядом написать их порядковые номера из натурального ряда чисел [7, с.78]:

Здесь каждому четному числу соответствует один порядковый номер из натурального ряда чисел и наоборот. Значит, утверждается, число четных чисел равно числу всех чисел натурального ряда.

Но это неверно. В частности, в данном примере четные числа не являются частью ряда натуральных чисел, это совершенно самостоятельный ряд, в котором вместо четных чисел могли быть любые символы.

Ошибка состоит в некорректном способе подсчета, в котором часть элементов исходного ряда просто игнорируется, исключается из процедуры подсчета. Произведём подсчет другим, правильным способом. Возьмем ряд всех натуральных чисел и будем их считать самым обычным, привычным способом. Для этого каждое натуральное число будем класть в соответствующий ящик, и при этом называть его значение: один, два, три и так далее. Одновременно, по мере того, как нам будут встречаться эти числа, мы будем с каждым четным числом класть такую же цифру во второй ящик. И, для наглядности, с каждым нечётным – в третий ящик. Ну, и для ещё большей наглядности – для каждого пятого числа – в четвертый ящик.

Через некоторое время посмотрим, что у нас в ящиках? Через тысячу шагов, очевидно, в первом ящике будет 1 000 чисел. Во втором и третьем – по 500, а в четвертом – только 200. Ну, или в виде соотношения 10:5:5:2.

Продолжим раскладывать числа и вновь проверим содержимое ящиков теперь уже через 10 000 шагов. И в этот раз мы обнаружим, что количества чисел в ящиках соотносятся как 10:5:5:2. Нужно ли доказывать, что и через миллион, и через миллиард, и через гугл шагов количества чисел в ящиках будут соотноситься как 10:5:5:2?

Если мы последовательно синхронно считаем количества чисел в натуральном ряду, то мы найдём истинное соотношение их количеств. Однако говорить, что бесконечное число всех натуральных чисел больше, чем число всех четных или нечетных чисел не совсем правильно. Эти числа образуют бесконечности, и следует говорить только об их мощности:

бесконечность всех натуральных чисел в два раза мощнее, чем бесконечности всех четных или нечетных чисел и в пять раз мощнее, чем бесконечность всех чисел, кратных пяти.

Утверждение, что часть может равняться целому ошибочно в самой формулировке. Мощность части бесконечности всегда меньше мощности всей бесконечности.

Рассмотрим приведённый выше пример в терминах мощностей. Примем без доказательства, что количество членов множества и его мощность – это разные, но схожие по смыслу понятия. Мы не можем сравнивать число членов множеств, по определению равных бесконечности, но мы можем сравнивать их мощности. Отношение мощностей М₁ и М₂ равномощных множеств всегда равно конечному числу:

В этом случае отношение множеств (1) для четных чисел запишется в виде:

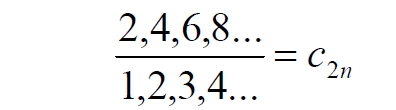
Запишем также и отношение множеств для нечетных чисел:

Далее нам понадобится и такое тождественное отношение:

Это равенство очевидно, поскольку числитель равен знаменателю. Теперь просуммируем эти приведенные два отношения мощностей:

Очевидно, что последняя дробь содержит в числителе все целые натуральные числа:

поэтому они и равны тождественно единице.

Это определённо означает, что мощности множеств всех натуральных чисел и суммы множеств всех четных и нечетных чисел равны. Но это также означает и тождественное равенство их бесконечного количества членов. Очевидно, что множества четных и нечетных чисел равномощны, поэтому, разделив полученное равенство на c_n, получим:

Поэтому из равенства также следует, что каждая из мощностей четных и нечётных чисел в два раза «слабее» мощности всех натуральных чисел:

Отметим также без доказательств, что любые действия над каждым членом множества не изменяют мощности множества:

Из этого непосредственно следует, что решающее значение имеет способ, каким получено множество. Например, множество всех четных чисел может быть получено удалением из множества всех натуральных чисел нечётных или умножением на 2 каждого члена множества всех натуральных чисел:

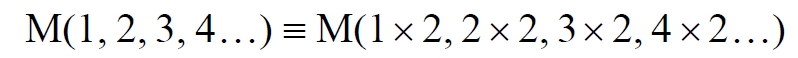
Казалось бы, последнее выражение является точной копией множества всех четных чисел М(2, 4, 6, 8…). Но это ошибочно, поскольку любые действия над всеми (или отдельными) членами множества не изменяют их полного количества и, соответственно, мощности. Поэтому справедливо (знак множества M опускаем):

Хотя оба множества в числителях в обеих строках выглядят тождественно, на самом деле это разные множества, имеющие разную мощность.

Перестановки в рядах. Еще один вариант доказательства равномощности части и целого приведен в книге [2, с.282], где предлагается вести подсчет нечетных чисел, предварительно переставив их в ряду: ...